Logistic Regression
Goals of the lecture
- Classification: dealing with categorical outcomes.
- Logistic regression.
- Why not linear regression?
- Generalized linear models (GLMs).
- Odds and log-odds.
- The logistic function.
- Building and interpreting logistic models with
glm.
What is classification?
“To classify is human…We sort dirty dishes from clean, white laundry from colorfast, important email to be answered from e-junk…. Any part of the home, school, or workplace reveals some such system of classification.”
— Bowker & Star, 2000
- Classification = predicting a categorical response variable using features
- Common examples:
- Is an email spam or not spam?
- Is a cell mass cancerous or not cancerous?
- Will this customer buy or not buy?
- Is a credit card transaction fraudulent?
- Is this image a cat, dog, person, or other?
Binary vs. multi-class classification
- Binary classification: sorting inputs into one of two labels
- E.g., spam vs. not spam
- Multi-class classification: more than two labels
- E.g., face recognition with n possible identities
- E.g., image classification (cat, dog, person, other)
- Today: focus on binary classification with logistic regression
Part 1: Foundations of logistic regression
Motivation, log-odds, and the logistic function.
Example dataset: Email spam
[1] 3921Why not linear regression?
spamis coded as 0 (no) or 1 (yes)- Could we treat this as continuous and use linear regression?
- Interpret prediction \(\hat{y}\) as probability of outcome?
💭 Check-in
What issues might arise here?
The problem: predictions beyond [0,1]
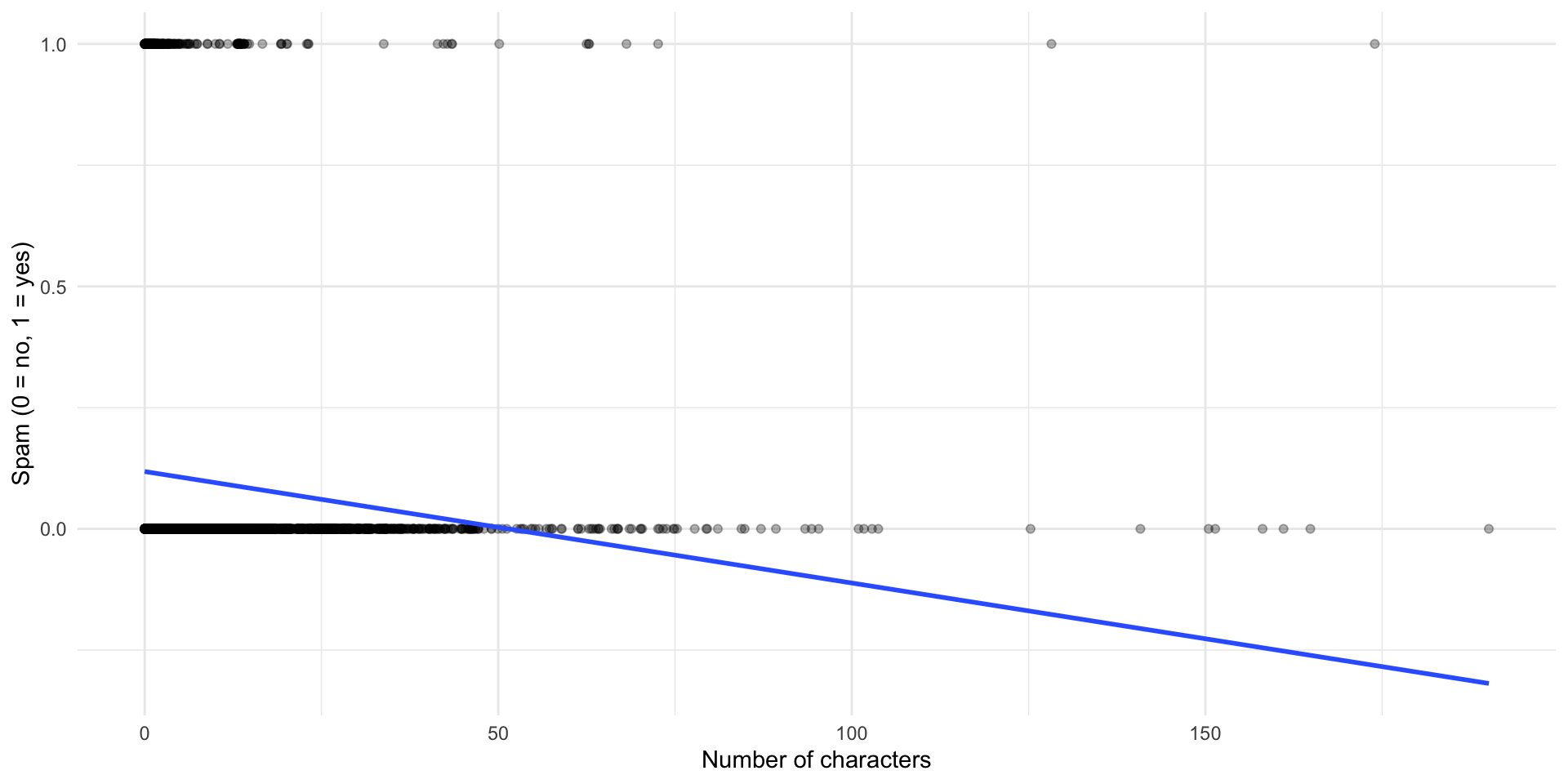
Linear model generates predictions outside [0,1], but probability must be bounded!
Framing the problem probabilistically
- Treat each outcome as Bernoulli trials: “success” (spam) vs. “failure” (not spam)
- Each observation has independent probability of success: \(p\)
- On its own: \(p\) = proportion of spam emails
- Goal: model \(p\) conditioned on other variables, i.e., \(P(Y = 1 | X)\)
Question: What does \(p\) on its own remind you of from linear regression?
Answer: The intercept-only model (the mean of \(Y\))
Generalized linear models (GLMs)
Generalized linear models (GLMs) are generalizations of linear regression.
Each GLM has:
- A probability distribution for the outcome variable
- A linear model: \(\beta_0 + \beta_1 X_1 + ... + \beta_k X_k\)
- A link function relating the linear model to the outcome
We need a function that links our linear model to a probability score bounded at [0, 1].
Common GLMs
| Model name | Distribution | Link function | Use cases | Example |
|---|---|---|---|---|
| Linear regression | Normal | Identity | Continuous response | Height, price |
| Logistic regression | Bernoulli/Binomial | Logit | Binary response | Spam, fraud |
| Poisson regression | Poisson | Log | Count data | # words, # visitors |
Today: logistic regression
The logit link function
Logistic regression uses the logit link function:
\[\text{logit}(p) = \log\left(\frac{p}{1-p}\right)\]
- Where \(p\) is the probability of some outcome
- Takes a value between \([0, 1]\) and maps it to \((-\infty, \infty)\)
- Also called the log-odds
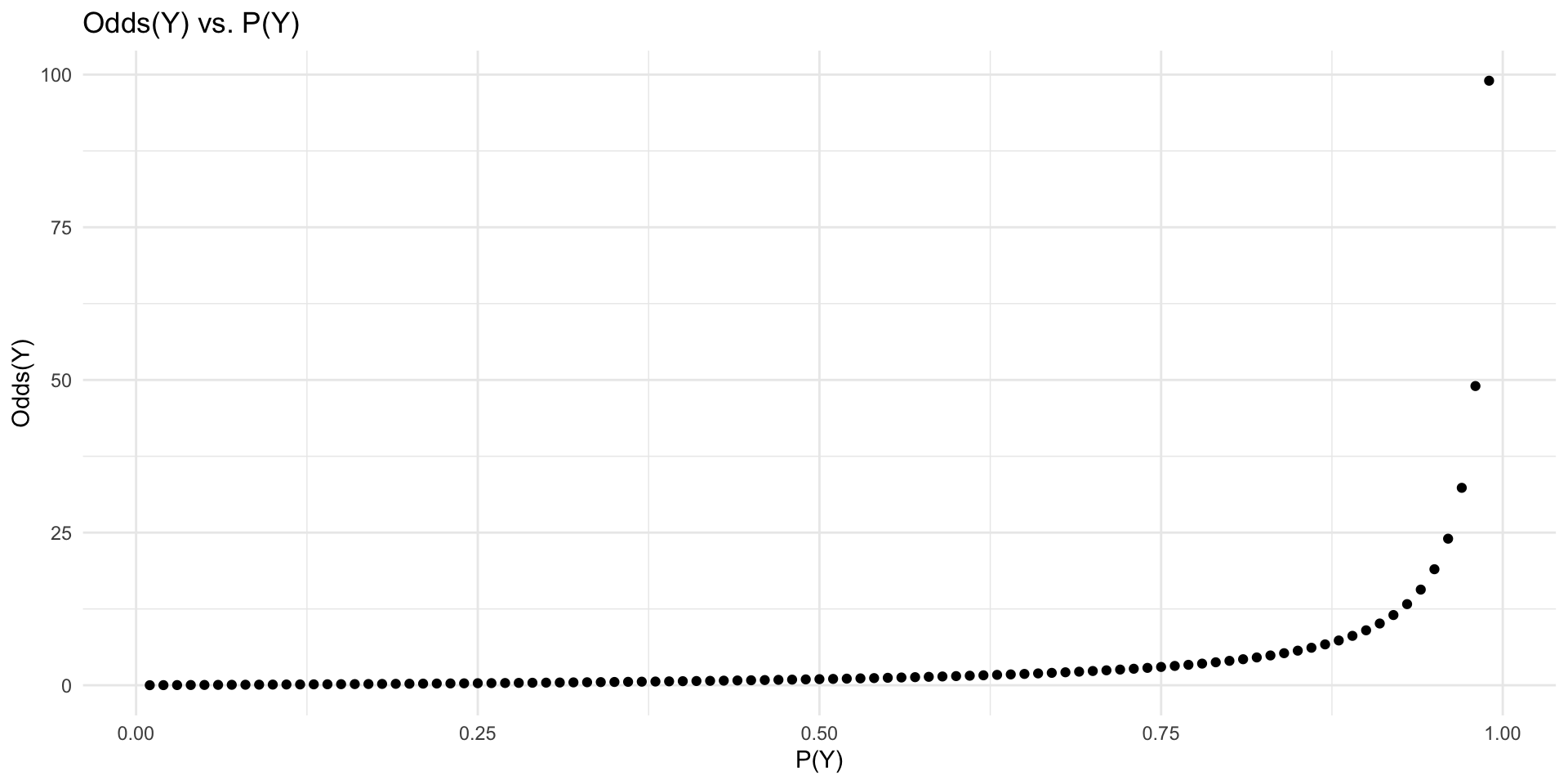
Introducing the odds
The odds of an event are the ratio of the probability of an event occuring (\(p\)) and the probability of event not occurring (\(1-p\)).
\[\text{Odds}(Y) = \frac{p}{1-p}\]
- Unlike \(p\), odds are bounded at \([0, \infty)\)
- Odds of 1 means 50/50 chance
- Odds > 1 means more likely to occur than not
- Odds < 1 means less likely to occur than not
Visualizing odds
Introducing the log-odds (logit)
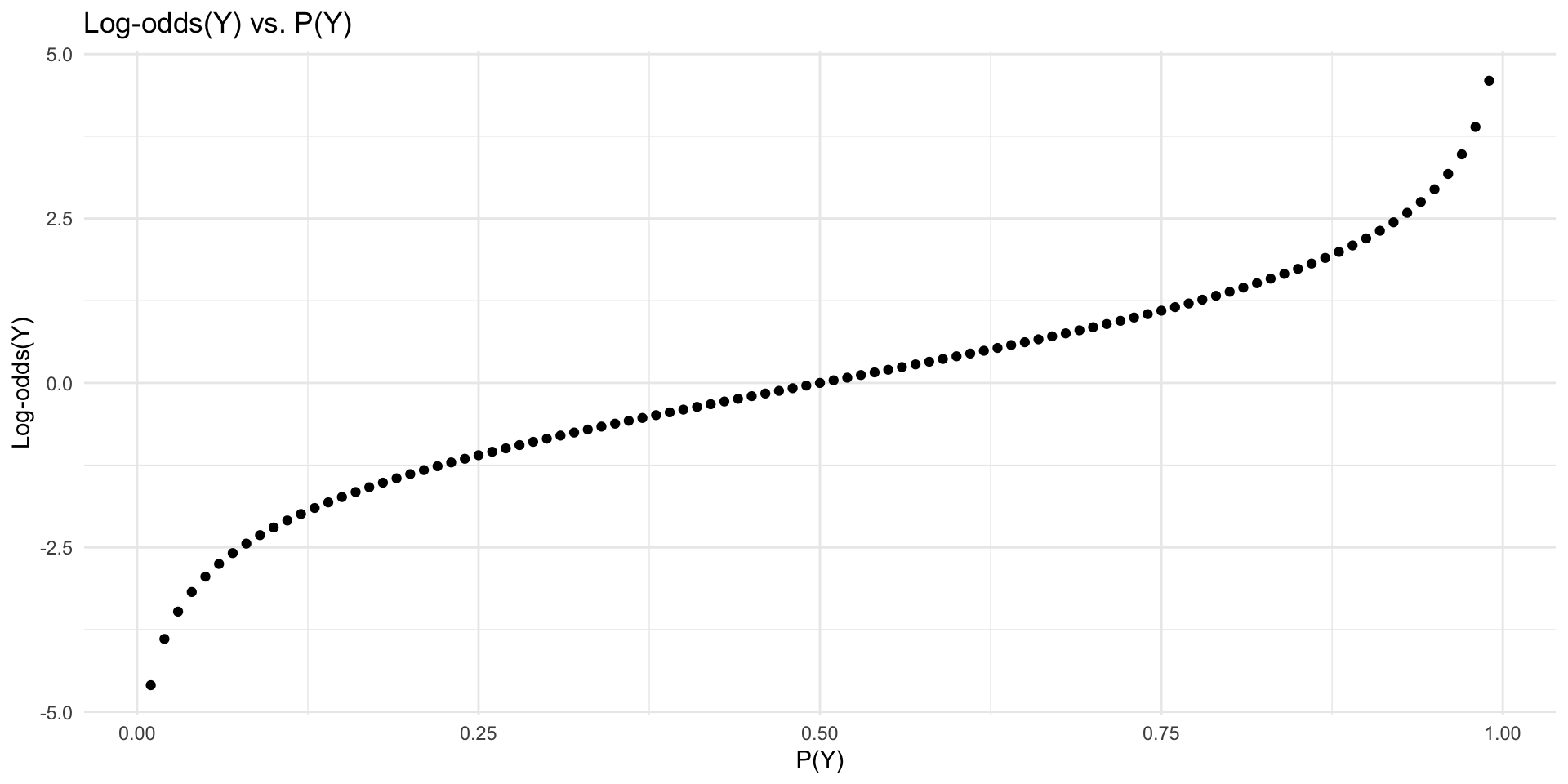
The log-odds is the log of the odds (the logit function).
\[\text{logit}(p) = \log\left(\frac{p}{1-p}\right)\]
- Unlike \(p\), log-odds are bounded at \((-\infty, \infty)\)
- This is what we’ll model linearly!
Visualizing log-odds
Interpreting the sign of log-odds
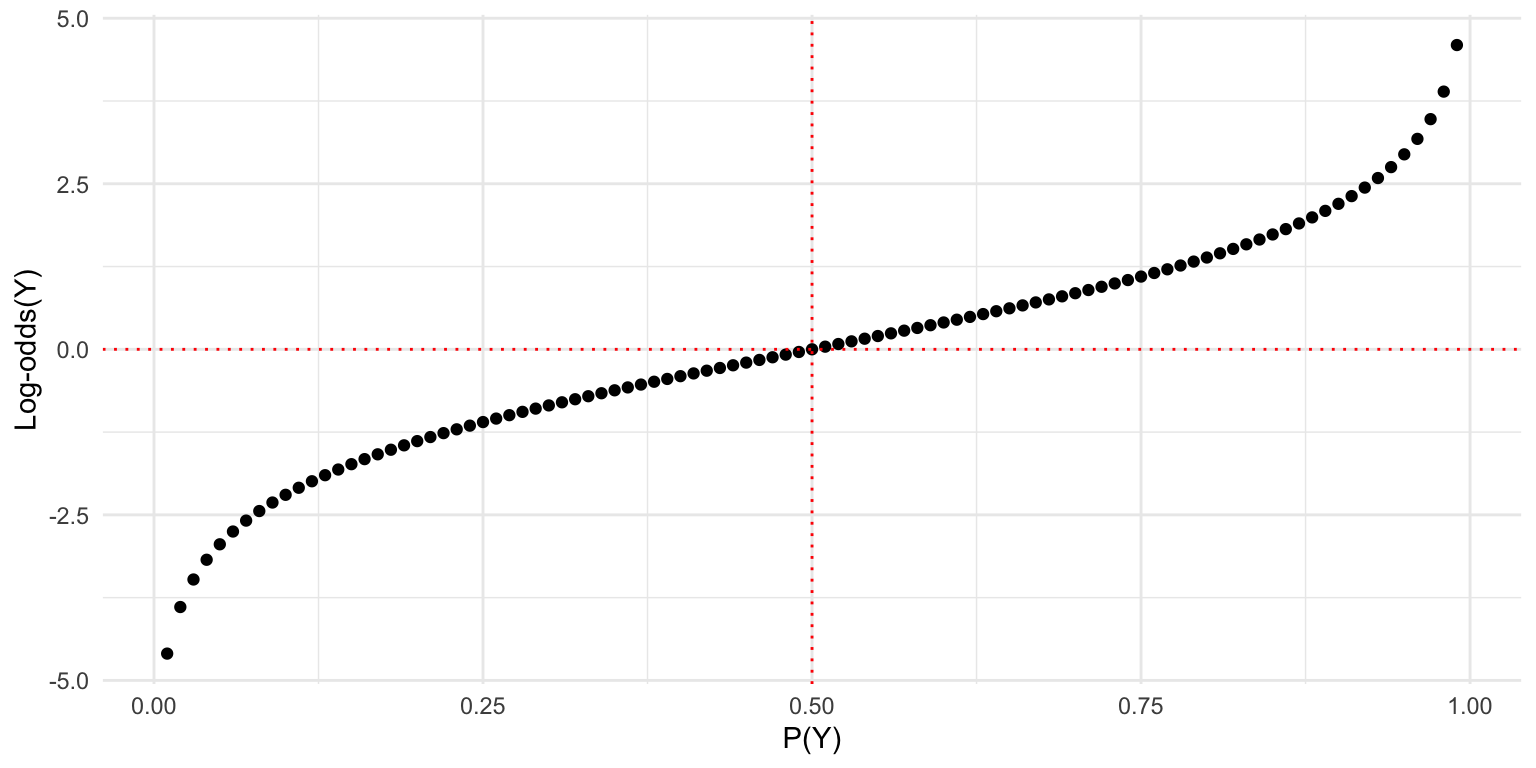
- Positive log-odds → \(p > 0.5\)
- Negative log-odds → \(p < 0.5\)
Is log-odds linearly related to p?
No! The log-odds of \(Y\) is non-linearly related to \(P(Y)\).
- This means we cannot interpret linear changes in log-odds as linear changes in probability
- This will be very important when interpreting logistic regression models
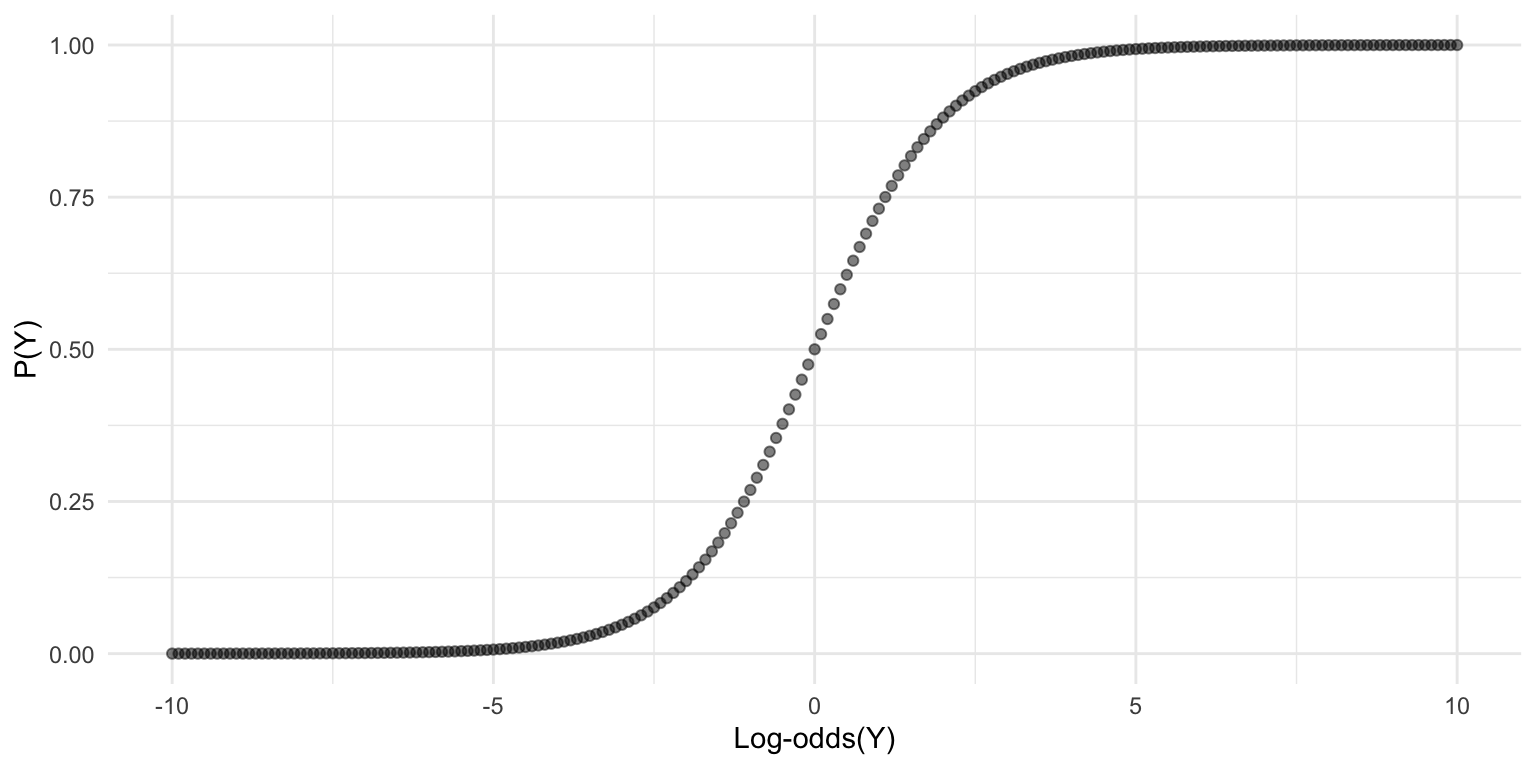
The logistic function
The logistic function is the inverse of the logit function.
\[P(Y) = \frac{e^{\text{logit}(p)}}{1 + e^{\text{logit}(p)}}\]
- Converts log-odds back to probability
- Maps \((-\infty, \infty)\) to \([0, 1]\)
- Also called the sigmoid function
Mapping from log-odds to probability
Where does regression come in?
With logistic regression, we learn parameters \(\beta\) for:
\[\log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 X_1 + ... + \beta_k X_k\]
- Our “dependent variable” is the log-odds (logit) of \(p\)
- We learn a linear relationship between \(X\) and the log-odds of our outcome
- NOT a linear relationship with probability itself!
Interpreting β: log-odds ~ X is linear
\[\log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 X\]
- If \(\beta_1 > 0\): For each 1-unit increase in \(X\), log-odds increase by \(\beta_1\)
- If \(\beta_1 < 0\): For each 1-unit increase in \(X\), log-odds decrease by \(|\beta_1|\)
- Straightforward linear interpretation for log-odds
Interpreting β: P(Y) ~ X is NOT linear
The mapping between log-odds and \(P(Y)\) is not linear.
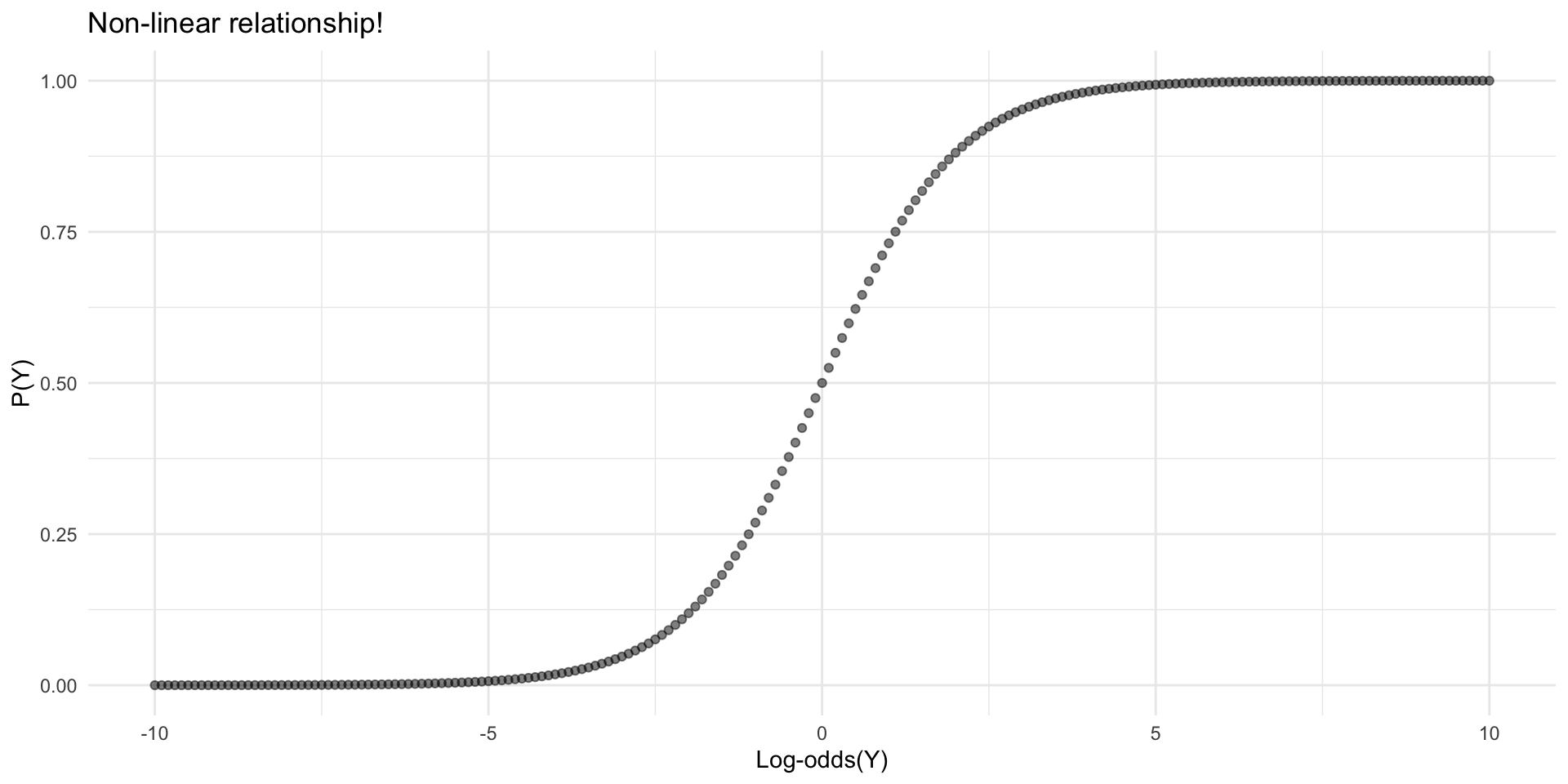
We cannot interpret coefficients linearly with respect to \(P(Y)\)!
Part 2: Logistic regression in R
Using glm, interpreting logistic models.
Logistic regression in R
Use the glm() function with family = binomial:
family = binomial: specifies we’re modeling binary outcomeslink = "logit": specifies the logit link function (default for binomial)- Fitting is straightforward—interpreting is the harder part!
Fitting a simple model
Let’s predict spam from num_char (message length):
Call:
glm(formula = spam ~ num_char, family = binomial, data = df_spam)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.798738 0.071562 -25.135 < 2e-16 ***
num_char -0.062071 0.008014 -7.746 9.5e-15 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2437.2 on 3920 degrees of freedom
Residual deviance: 2346.4 on 3919 degrees of freedom
AIC: 2350.4
Number of Fisher Scoring iterations: 6Interpreting the coefficients
- Intercept (-1.80): log-odds of spam when
num_char = 0 - num_char (-0.06): for every 1-unit increase in
num_char, log-odds of spam decrease by 0.06 - Negative coefficient → longer emails are less likely to be spam
Converting log-odds to probability
What’s \(P(\text{spam})\) when num_char = 0?
(Intercept)
-1.798738 (Intercept)
0.1420048 About 14% chance of spam for a message with 0 characters.
Example: num_char = 100
What’s \(P(\text{spam})\) when num_char = 100?
(Intercept)
-8.005853 (Intercept)
0.0003333936 Less than 0.1% chance—very unlikely to be spam!
Visualizing: log-odds vs. probability
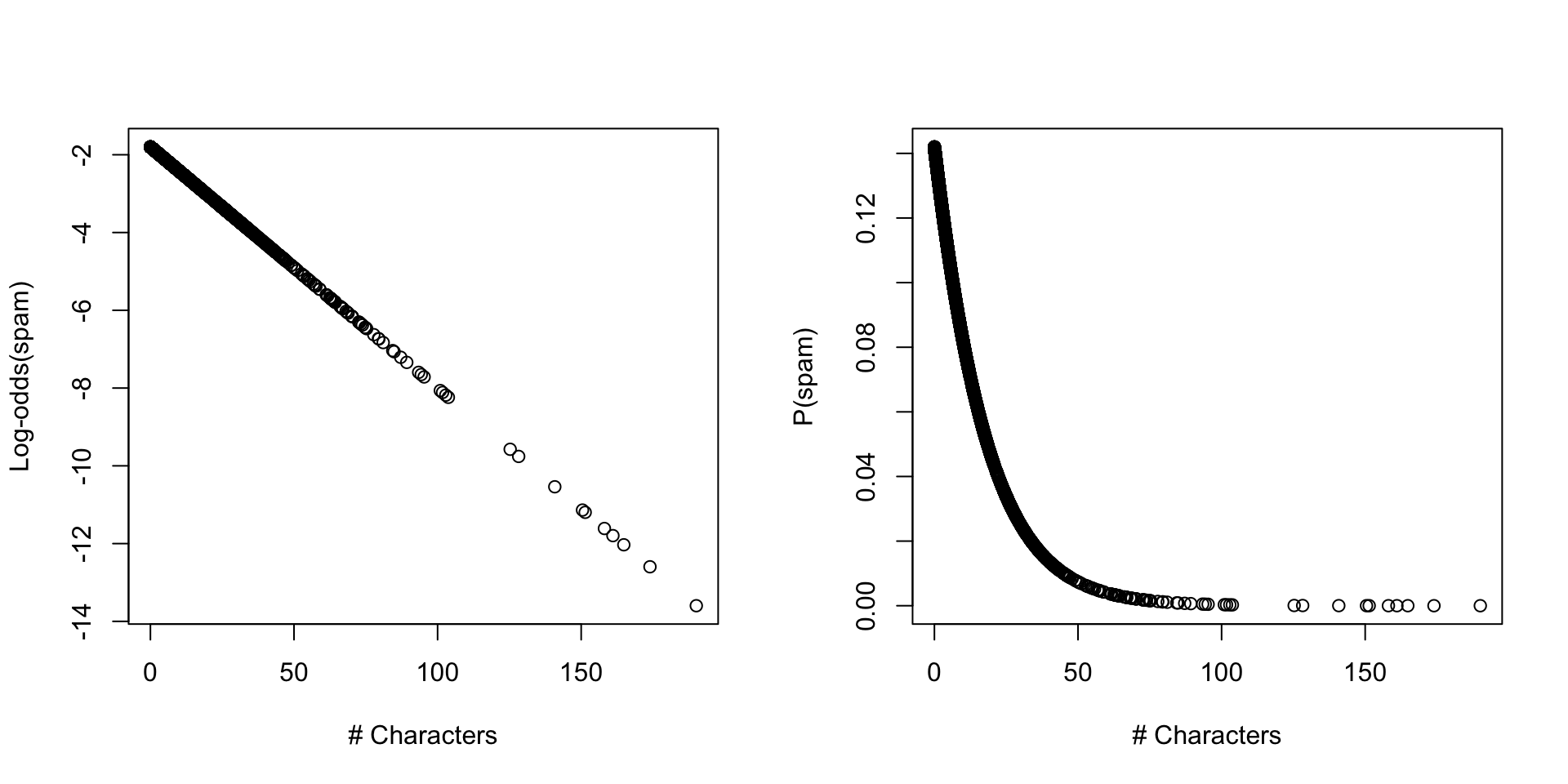
Linear on log-odds scale, non-linear on probability scale!
Categorical predictors
Let’s use winner (whether email contains the word “winner”):
Call:
glm(formula = spam ~ winner, family = binomial, data = df_spam)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.31405 0.05627 -41.121 < 2e-16 ***
winneryes 1.52559 0.27549 5.538 3.06e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2437.2 on 3920 degrees of freedom
Residual deviance: 2412.7 on 3919 degrees of freedom
AIC: 2416.7
Number of Fisher Scoring iterations: 5Interpreting categorical predictors
- Intercept (-2.31): log-odds of spam when
winner = "no" - winneryes (1.53): change in log-odds (relative to intercept) when
winner = "yes" - Just like linear regression: categorical predictors are relative to reference level
Probability for winner = “no”
(Intercept)
0.0899663 About 9% chance of spam without “winner”
Probability for winner = “yes”
(Intercept)
0.3125 About 31% chance of spam with “winner”—much higher!
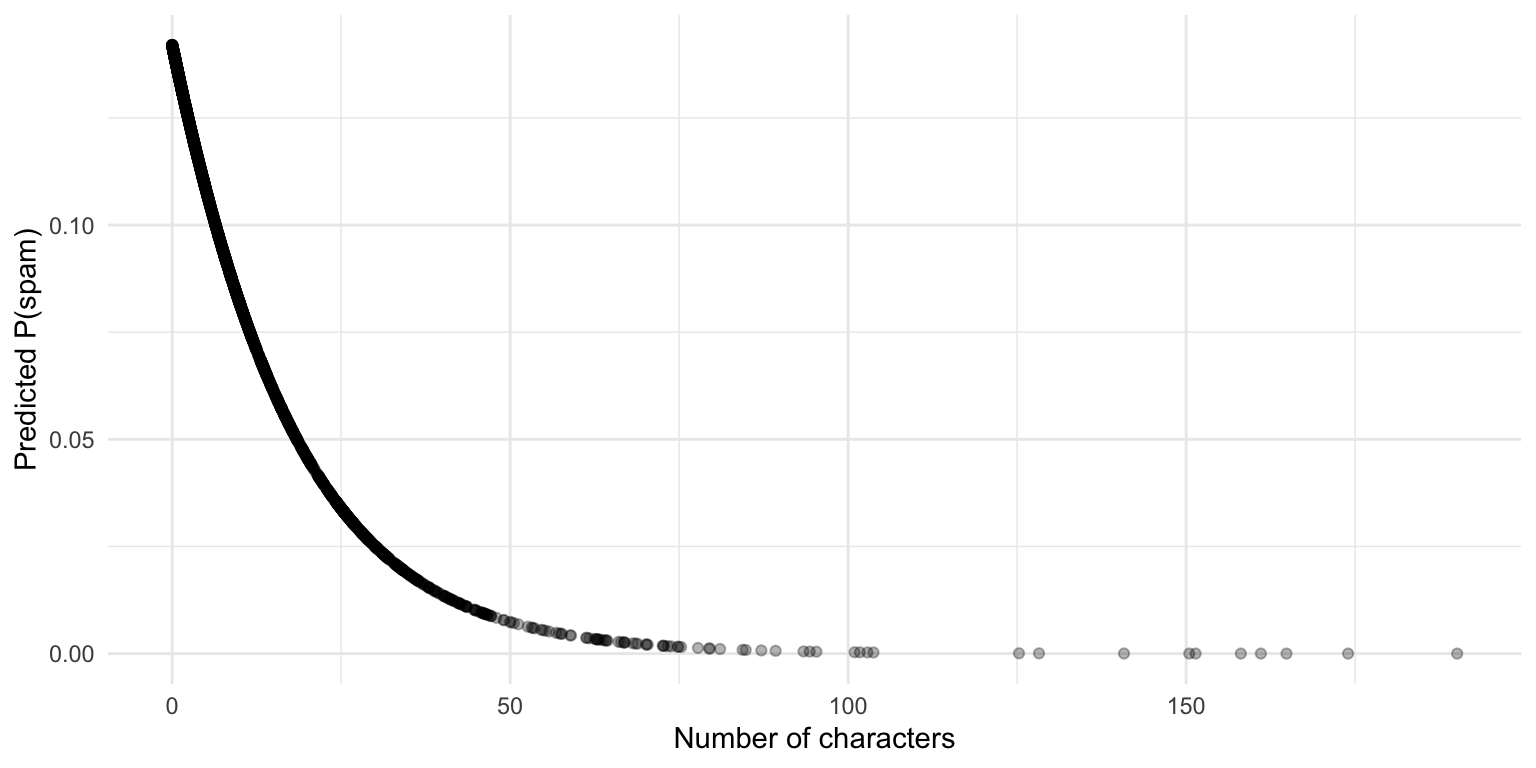
Generating predictions
The predict() function with type = "response" gives predicted \(P(Y)\):
Summary
- Many statistical modeling problems involve categorical response variables
- Logistic regression for binary classification tasks
- It’s a generalized linear model (GLM)
- Predicts log-odds of \(P(Y)\) as a linear function of \(X\)
- Log-odds converted to \(P(Y)\) using the logistic function
- Interpretation:
- Linear relationship with log-odds
- Non-linear relationship with probability
CSS 211 | UC San Diego